SEQUENCE
A sequence, in mathematics, is a string of objects, like numbers, that follow a particular pattern. The individual elements in a sequence are called terms. Some of the simplest sequences can be found in multiplication tables:
- 3, 6, 9, 12, 15, 18, 21, …
Pattern: “add 3 to the previous number to get the next number”
- 0, 12, 24, 36, 48, 60, 72, …
Pattern: “add 12 to the previous number to get the next number”
Of course we can come up with much more complicated sequences:
- 10,–2 8,×2 16,–2 14,×2 28,–2 26,×2 52, …
Pattern: “alternatingly subtract 2 and multiply by 2 to get the next number”
- 0,+2 2,+4 6,+6 12,+8 20,+10 30,+12 42, …
Pattern: “add increasing even numbers to get the next number”
We can also create sequences based on geometric objects:
Pattern: “add 3 to the previous number to get the next number”
Pattern: “add 12 to the previous number to get the next number”
Pattern: “alternatingly subtract 2 and multiply by 2 to get the next number”
Pattern: “add increasing even numbers to get the next number”
Triangle Numbers
Pattern: “add increasing integers to get the next number”
| |||||
1
|
3
|
6
|
10
|
15
|
Square Numbers
Pattern: “add increasing odd numbers to get the next number”
|
Note that the sequences of triangle and square numbers also have numerical patterns like the ones we saw at the beginning. To find the following triangle numbers we have to add increasing integers to the last term of the sequence (+2, +3, +4, …). To find the following square numbers we have to add increasing odd numbers (+3, +5, +7, …).
EXAMPLES FOR PATTERNS AND SEQUENCE
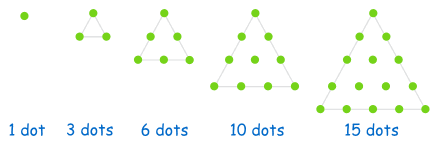
Triangular Numbers
| 1, 3, 6, 10, 15, 21, 28, 36, 45, ... |
Its is generated from a pattern of dots which form a triangle.
By adding another row of dots and counting all the dots we can find the next number of the sequence:
Square Numbers
| 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
They are the squares of whole numbers:
0 (=0×0)
1 (=1×1)
4 (=2×2)
9 (=3×3)
16 (=4×4)
etc...
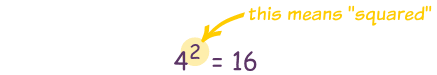
This says "4 Squared equals 16"
(the little 2 says the number appears twice in multiplying)
1 (=1×1)
4 (=2×2)
9 (=3×3)
16 (=4×4)
etc...
Example: What is 3 squared?
| 3 Squared | = |  | = 3 × 3 = 9 |
"Squared" is often written as a little 2 like this:
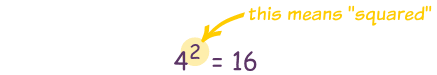
This says "4 Squared equals 16"
(the little 2 says the number appears twice in multiplying)
Squares From 12 to 62
| 1 Squared | = | 12 | = | 1 × 1 | = | 1 |
| 2 Squared | = | 22 | = | 2 × 2 | = | 4 |
| 3 Squared | = | 32 | = | 3 × 3 | = | 9 |
| 4 Squared | = | 42 | = | 4 × 4 | = | 16 |
| 5 Squared | = | 52 | = | 5 × 5 | = | 25 |
| 6 Squared | = | 62 | = | 6 × 6 | = | 36 |
Cube Numbers
| 1, 8, 27, 64, 125, 216, 343, 512, 729, ... |
They are the cubes of the counting numbers (they start at 1):
1 (=1×1×1)
8 (=2×2×2)
27 (=3×3×3)
64 (=4×4×4)
etc...
8 (=2×2×2)
27 (=3×3×3)
64 (=4×4×4)
etc...
Cubes and Cube Roots
To understand cube roots, first we must understand cubes ...
How to Cube A Number
To cube a number, just use it in a multiplication 3 times ...
Example: What is 3 Cubed?
| 3 Cubed | = | 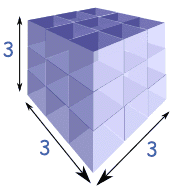 | = | 3 × 3 × 3 | = | 27 |
Note: we write down "3 Cubed" as 33
(the little 3 means the number appears three times in multiplying)
(the little 3 means the number appears three times in multiplying)
Some More Cubes
| 4 cubed | = | 43 | = | 4 × 4 × 4 | = | 64 |
| 5 cubed | = | 53 | = | 5 × 5 × 5 | = | 125 |
| 6 cubed | = | 63 | = | 6 × 6 × 6 | = | 216 |
Cube Root
A cube root goes the other direction:
3 cubed is 27, so the cube root of 27 is 3
| 3 |  | 27 |
The cube root of a number is ...
... a special value that when cubed gives the original number.
... a special value that when cubed gives the original number.
The cube root of 27 is ...
... 3, because when 3 is cubed you get 27.
... 3, because when 3 is cubed you get 27.
 |
Note: When you see "root" think
"I know the tree, but what is the root that produced it?"
In this case the tree is "27", and the cube root is "3".
|
Here are some more cubes and cube roots:
 | ||
4
|
64
| |
5
|
125
| |
6
|
216
| |
References:
No comments:
Post a Comment